 切り絵 「縁切り橋の縁結び」
切り絵 「縁切り橋の縁結び」
問題を解くときに式を書こうとしない子がいます。単に面倒だという理由なのでしょうが,式を書かないことにはデメリットしかありません。頭の中だけでは処理できない難度の高い問題では,問題文を読みながら少しずつ計算を進め,問題を解くための条件を式を書きながら自分で作り出す場合が多いのですが,日頃から式を書く習慣のない子が応用問問題をほとんど解けないのはその作業をしないからです。わたしはよく「式を書きなさい」と言います。
次の問題を例にしてみます。やや上級レベルの問題です。
図のようなA地点からB地点まで行くのに21分,B地点からA地点に戻るのに19分かかりました。上りは分速60m,下りは分速90mで歩きました。AB間は何mですか。
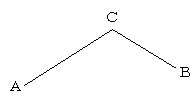
この問題の解き方はいろいろあります。いくつか並べてみます。
<解法1>AC間=χm,BC間ymとします。距離を速さで割り,時間を求める式を立てます。
![]()
これは連立方程式です。中学生になるとこの方法でやるようになります。このあとは通分して計算することになりますが,やや計算が面倒です。
<解法2>上りと下りの速さ比が60:90=2:3なので,同じところの上り下りにかかる時間比は3:2と なることを利用します。AC間の上りにかかった時間を③とすると,下りにかかった時間は②,BC間の上りにかかった時間を<3>とすると,下りにかかった時間は<2>です。これを使って式を立てます。
③+<2>=21,<3>+②=19
これも連立方程式です。これを解くと①=5(分)<1>=3(分)となり,AC間を求めることができます。
<解法3>上りと下りにかかった時間の比は,3:2です。往復で21+19=40分かかっていますから,上りだけにかかった時間を次のように求めることができます。私はこの方法を使っています。
![]() ・・・上りにかかった時間
・・・上りにかかった時間
合計24分上っているので,60×24=1440(m)がAB間の距離です。解くことができればよいので,どの方法でもかまいません。入試問題だと,さらにAC間の距離を求めさせる流れになりますが,ここでは省略します。
成績優秀者は,このような問題を解くときに必ずきれいに式を書きます。式を書きながら頭を整理しているので,次に何をやればいいのかわかってきます。当然,ミスは少ないです。
どの方法であっても,式をきれいに書き進めないで筆算だけで済まそうとすると,途中で思考が混乱したり,筆算の数字を見間違えたりするミスが出たりして,正解にたどり着けなくなります。式を書く作業は,自分の思考の整理です。それを面倒だと感じているようでは算数は上達しません。天才は別ですが・・・
ご意見ご感想を書いていただけるよう、何とか設定できました(^o^)

プロフィールと最近の投稿はサイドバーで。挿し絵はすべて自作したものです。

