前々回,暗算の重要性について書きましたが,それに関連して円周率の計算について触れたいと思います。円の面積は「半径×半径×3.14」で求めますが,この「半径×半径」の部分が2けたの積になることがよくあります。よく見られるのが「12×12」「15×15」「16×16」などです。そこで,「11×11」から「16×16」あたりまでは暗記しておくようにすると楽です。12×12=144,15×15=225などはよく出てくる計算です。これらを暗記しておくと,他の問題で役に立つことも多々あります。
ついでですが,□5×□5という形のかけ算も覚えておくと楽です。まず,□×(□+1)の答えを百の位にして,下2けたは25とします。たとえば,25×25だと,2×3=6が百の位,下2けたは25なので25×25=625です。65×65だと,6×7=42が百の位,下2けたは25で,答えは4225です。他の例も確認してみてください。
じつは,十の位が同じで,一の位の和が10になる2けたの積は同じようにできるのですが,あまり実用性はないのでそこまで無理に覚える必要はないと思います。(46×44=2024,72×78=5616など)
では円周率を使った計算ですが,まず,314×2から314×9の答えを暗記しておきましょう。314×2=628,314×3=942,314×4=1256,314×5=1570,314×6=1884,314×7=2198,314×8=2512,314×9=2826です。
小学校では小数のかけ算を練習させるために3.14を使った筆算をさせますが,上の計算を暗記しておけば円の面積の計算は楽になります。たとえば,「半径8cmの円の面積を求めなさい」という問題だと、8×8×3.14という計算をすることになりますが,下のように4をかけたときは1256と,6をかけたときは1884と,覚えている数字を書くだけです。ここで筆算をする必要はありません。素早く処理ができてミスも減ります。3.14を上の段に書き,半径×半径で求めた数字を下の段に書くようにします。
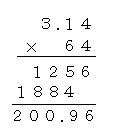
次回は「単位について」書く予定でしたが,ちょっと雰囲気を変えて「伸びる子の特徴」というものを考えてみようかなと思っています。

プロフィールと最近の投稿はサイドバーで。挿し絵はすべて自作したものです。

